Wahrscheinlichkeit Fehler 2. Art - Vertiefung der Statistik - Fernuni Hagen
Vertiefung Statistik-Paket > Vertiefung-Statistik > Vertiefung statistischer Verfahren
Voraussetzungen zur Berechnung der Wahrscheinlichkeit des Fehlers 2. Art (𝜷-Fehler):
Unter bestimmten Voraussetzungen ist es möglich, die Wahrscheinlichkeit des Fehlers 2. Art, den 𝛽-Fehler, zu berechnen. Es bedarf der folgenden Voraussetzungen, um die Berechnung der Wahrscheinlichkeit eines 𝛽-Fehler zu ermöglichen:
1. Der 𝛽-Fehler kann nur unter der Annahme der Gültigkeit der Alternativhypothese 𝐻_1 berechnet werden
2. Die Alternativhypothese 𝐻_1 muss vereinfacht sein und auf einen bestimmten Wert lauten
Unter diesen Voraussetzungen ist der 𝛽-Fehler die Wahrscheinlichkeit, dass die Prüfgröße/Teststatistik in den Nicht-Ablehnungsbereich der Nullhypothese fällt.
Merke: Die Annahme der Gültigkeit der Alternativhypothese setzt eigentlich voraus, den wahren unbekannten Parameterwert zu kennen, denn die Fehlerwahrscheinlichkeit 𝛼 der Alternativhypothese wird ausgeschlossen. Zusätzlich lautet eine Alternativhypothese normalerweise nicht nur auf einen Wert, sondern umfasst die Komplementärmenge der Nullhypothese. Die getroffenen Annahmen entsprechen also nicht in dem Sinne den statistischen Testverfahren, weshalb die eigentliche Unbekanntheit des 𝛽-Fehlers bei statistischen Testverfahren bestehen bleibt.
ACHTUNG: Die folgenden Ausführungen zur Berechnung und Betrachtung des 𝛽-Fehlers sind nur für den unbekannten Parameter 𝜇 gültig.
Grafische Veranschaulichung der Wahrscheinlichkeit des 𝜷-Fehlers für den zweiseitigen Gauß-Test:
Durch die Vereinfachungen, dass die Alternativhypothese auf einen bestimmten Wert lautet und der Annahme, dass die Alternativhypothese gültig ist, lässt sich eine Dichtefunktion um den Erwartungswert 𝜇 der Alternativhypothese legen. Die Wahrscheinlichkeit des 𝛽-Fehlers ist nun die Fläche der Dichtefunktion der Alternativhypothese, die im Nicht-Ablehnungsbereich der Nullhypothese liegt:
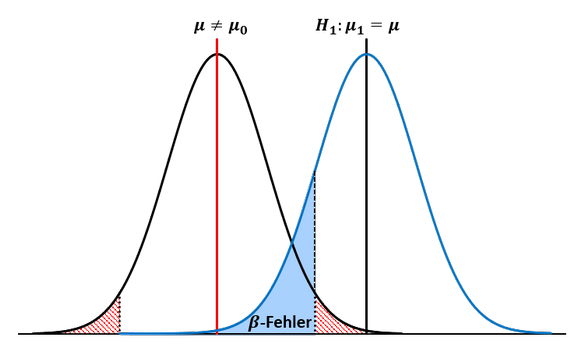
Allgemeine Berechnung der Wahrscheinlichkeit des Fehlers 2. Art (𝜷-Fehler) bei zweiseitigem Gauß-Test:
Zur Berechnung der Wahrscheinlichkeit des Fehlers 2. Art bei einem zweiseitigen Gauß-Test ist der Flächeninhalt der Dichtefunktion der Alternativhypothese zu berechnen, welcher innerhalb des Nicht-Ablehnungsbereichs der Nullhypothese liegt. Dazu wird der Erwartungswert der Alternativhypothese 𝜇_1 = 𝜇 über den Erwartungswert der Nullhypothese standardisiert und die kritischen Werte des Testverfahrens werden im Verhältnis an den standardisierten Erwartungswert der Alternativhypothese durch Subtraktion angepasst. Die Wahrscheinlichkeit bis zum unteren kritischen Wert ist dann von der Wahrscheinlichkeit bis zum oberen kritischen Wert abzuziehen, um zur Wahrscheinlichkeit des 𝛽-Fehlers zu gelangen:
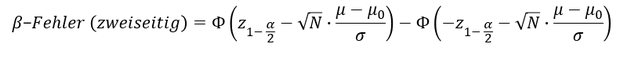
Merke: Der griechische Großbuchstabe Phi Φ bedeutet, dass die in den Klammern vorhandenen Werte in Wahrscheinlichkeiten der Standardnormalverteilung zu transformieren sind. Die in den Klammern berechneten Werte können also als z-Werte angesehen werden, deren Wahrscheinlichkeit vor der Subtraktion bestimmt werden muss.
Allgemeine Berechnung der Wahrscheinlichkeit des Fehlers 2. Art (𝜷-Fehler) bei einseitigem Gauß-Test:
Im Falle eines einseitigen Testverfahrens gilt es nur jeweils einen oberen oder unteren kritischen Wert zu verschieben. Die Berechnung der Wahrscheinlichkeit des Fehlers 2. Art gilt es dann entsprechend anzupassen:
Wahrscheinlichkeit des 𝜷-Fehlers bei einseitigem Testverfahren mit unterem kritischen Wert (𝑯_𝟎: 𝝁 ≥ 𝝁_𝟎 ):
Im Falle eines unteren kritischen Wertes befindet sich der gesamte Nicht-Ablehnungsbereich oberhalb des unteren kritischen Wertes. Entsprechend gilt es zur Ermittlung der Wahrscheinlichkeit des 𝛽-Fehlers die Wahrscheinlichkeit der Dichtefunktion der Alternativhypothese zu berechnen, dass die Prüfgröße/Teststatistik einen Wert größer als die untere Grenze annimmt. Dazu wird der Erwartungswert der Alternativhypothese 𝜇_1 = 𝜇 über den Erwartungswert der Nullhypothese standardisiert und der untere kritische Wert des Testverfahrens wird im Verhältnis an den standardisierten Erwartungswert der Alternativhypothese durch Subtraktion angepasst. Die Wahrscheinlichkeit bis zum unteren kritischen Wert ist dann von der Gesamtwahrscheinlichkeit 1 abzuziehen, um zur Wahrscheinlichkeit des 𝛽-Fehlers zu gelangen:
Wahrscheinlichkeit des 𝜷-Fehlers bei einseitigem Testverfahren mit oberem kritischen Wert (𝑯_𝟎: 𝝁 ≤ 𝝁_𝟎 ):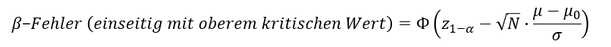
Im Falle eines oberen kritischen Wertes befindet sich der gesamte Nicht-Ablehnungsbereich unterhalb des oberen kritischen Wertes. Entsprechend gilt es zur Ermittlung der Wahrscheinlichkeit des 𝛽-Fehlers die Wahrscheinlichkeit der Dichtefunktion der Alternativhypothese zu berechnen, dass die Prüfgröße/Teststatistik einen Wert kleiner als die obere Grenze annimmt. Dazu wird der Erwartungswert der Alternativhypothese 𝜇_1 = 𝜇 über den Erwartungswert der Nullhypothese standardisiert und der obere kritische Wert des Testverfahrens wird im Verhältnis an den standardisierten Erwartungswert der Alternativhypothese durch Subtraktion angepasst. Die Wahrscheinlichkeit bis zum oberen kritischen Wert entspricht dann der Wahrscheinlichkeit des 𝛽-Fehlers:
Video "Wahrscheinlichkeit Fehler 2. Art":
Das Probe-Video behandelt die Thematik "Wahrscheinlichkeit Fehler 2. Art" des Kurses "Vertiefung der Statistik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Rechenbeispiel der Wahrscheinlichkeit des 𝜷-Fehlers bei zweiseitigem Gauß-Test:
Es sei die Nullhypothese 𝐻_0: 𝜇 = 𝜇_0 = 5 gegeben, wobei für die Alternativhypothese 𝐻_1 gilt, dass 𝐻_1: 𝜇_1 = 𝜇 = 6 ist. Welche Wahrscheinlichkeit nimmt der Fehler 2. Art an, wenn von einer bekannten Varianz 𝜎^2 = 4 bei einem Stichprobenumfang von 𝑁 = 25 und einem Signifikanzniveau von 𝛼 = 0,05 ausgegangen wird?
Lösung:
Da die Alternativhypothese dem tatsächlichen unbekannten Parameter 𝜇_1=𝜇=6 entspricht, gilt es diesen Wert mittels dem Erwartungswert der Nullhypothese zu standardisieren und die kritischen Werte beim Signifikanzniveau von 𝛼 = 0,05 anzupassen. Die Subtraktion der Wahrscheinlichkeit des unteren kritischen Wertes vom oberen kritischen Wert in der Standardnormalverteilung ergibt dann die Wahrscheinlichkeit des Fehlers 2. Art (𝛽-Fehler):

Der Fehler 2. Art (𝛽-Fehler) würde mit einer Wahrscheinlichkeit von 29,46% im Testverfahren eintreten.
Merke: Die Tabelle der Standardnormalverteilung geht nur bis zu einem 𝑧-Wert von 𝑧 = 3. Ab einem 𝑧-Wert von 3,9 ergibt sich die Wahrscheinlichkeit gerundet zu 1.
Grafische Veranschaulichung:
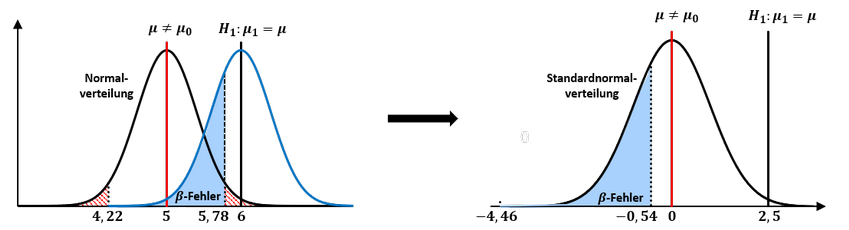
Vertiefung Statistik-Paket
Das Vertiefung Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Vertiefung der Statistik" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 140 Übungsaufgaben, Übungsklausuren und zur Auffrischung statistischer Grundkenntnisse das "Grundlagen Statistik-Paket" zur Verfügung.


