Theorem von Bayes - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Wahrscheinlichkeitsrechnung
Grundlage des Theorems von Bayes:
Mit dem Theorem von Bayes lässt sich das vorausgesetzte Ereignis bei einer angegebenen bedingten Wahrscheinlichkeit umkehren. Das bedeutet, dass wenn die bedingte Wahrscheinlichkeit von Ereignis 𝐵 unter der Bedingung von Ereignis 𝐴 (𝐵|𝐴) angegeben ist, sich mit dem Theorem von Bayes die bedingte Wahrscheinlichkeit zu (𝐴|𝐵) umkehren lässt bzw. es erfolgt eine Umkehr des vorausgesetzten Ereignisses. In Anlehnung an ein Venn-Diagramm soll die folgende Abbildung den Sachverhalt graphisch veranschaulichen:
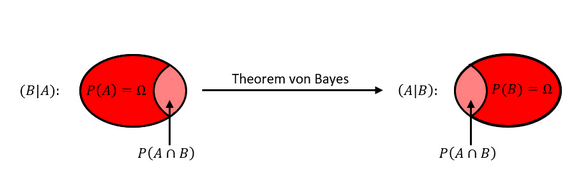
Allgemeine Berechnung des Theorems von Bayes:
Zur Berechnung des Theorems von Bayes muss sowohl die bedingte Wahrscheinlichkeit 𝑃(𝐵│𝐴) / 𝑃(𝐴|𝐵) als auch die Wahrscheinlichkeit des zuvor eingetretenen Ereignisses selbst 𝑃(𝐴) / 𝑃(𝐵) bekannt sein. Zusätzlich muss auch die bedingte Wahrscheinlichkeit für das Komplementärereignis 𝑃(𝐵|𝐴 ̅) / 𝑃(𝐴|𝐵 ̅) bekannt sein und dessen Eintrittswahrscheinlichkeit selbst 𝑃(𝐴 ̅) / 𝑃(𝐵 ̅). Mit dem Wissen über diese Sachverhalte kann mittels der Formel aus dem Theorem von Bayes die bedingte Wahrscheinlichkeit wie folgt umgedreht werden:

Konzeption des Theorems von Bayes:
Um zu verstehen, wie der Wechsel des gegebenen Ereignisses im Theorem von Bayes erfolgt, müssen wir uns die Konzeption der Formel ansehen. Der Zähler in der Formel des Theorems von Bayes ist so zusammengesetzt, dass man mittels des Multiplikationssatzes die bedingte Wahrscheinlichkeit im Zähler rückgängig macht, um zur Schnittmenge der Ereignisse P(𝐴∩𝐵) zu gelangen:
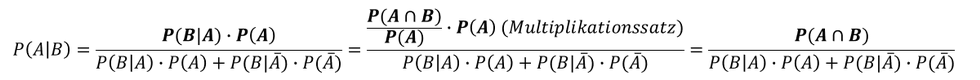
Der Nenner dagegen besteht aus zwei Multiplikationssätzen. Der linke Multiplikationssatz berechnet wiederrum die Schnittmenge von P(𝐴∩𝐵) wie im Zähler. Der rechte Multiplikationssatz berechnet die Schnittmenge P(¯𝐴∩𝐵), also die Schnittmenge mit dem Komplementärereignis. Addiert man die Schnittmenge eines Ereignisses P(𝐴∩𝐵) und dessen Komplementärschnittmenge P(¯𝐴∩𝐵), ergibt sich die Wahrscheinlichkeit 𝑃(𝐵), was folgende Abbildungen graphisch veranschaulichen:

Für die Formel des Theorems von Bayes gilt schließlich:
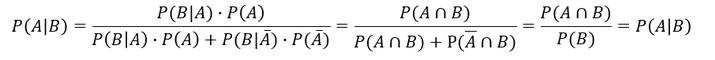
Die Umkehrung des vorausgesetzten Ereignisses im Theorem von Bayes erfolgt durch die Zurückrechnung der bedingten Wahrscheinlichkeit im Zähler und der Berechnung der Wahrscheinlichkeit des anderen Ereignisses im Nenner, was der Formel der bedingten Wahrscheinlichkeit für das andere Ereignis entspricht.
Video "Theorem von Bayes":
Das Probe-Video behandelt die Thematik "Theorem von Bayes" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Beispiel für das Theorem von Bayes:
Das Theorem von Bayes lässt sich in der Praxis mittels eines Beispiels veranschaulichen. Dabei wollen wir davon ausgehen, dass 50 Euro-Scheine mittels eines Geräts auf Echtheit geprüft werden. Dabei weiß man, dass 15 von 10000 Geldscheinen gefälscht sind. Durch Aufblinken signalisiert das Gerät, dass der Schein als falsch eingestuft wird. Die Wahrscheinlichkeit, dass das Gerät aufblinkt, wenn der Schein falsch ist, liegt bei 0,95. Die Wahrscheinlichkeit, dass das Gerät aufblinkt, wenn der Schein echt ist, liegt bei 0,1. Wir wollen den Ereignissen „Schein echt/unecht“ und „Aufblinken/Nicht Aufblinken des Geräts“ folgende Symboliken zuordnen:
𝐴 = 𝑆𝑐ℎ𝑒𝑖𝑛 𝑒𝑐ℎ𝑡 ; 𝐴 ̅ = 𝑆𝑐ℎ𝑒𝑖𝑛 𝑢𝑛𝑒𝑐ℎ𝑡 ; 𝐵 = 𝐴𝑢𝑓𝑏𝑙𝑖𝑛𝑘𝑒𝑛 𝑑𝑒𝑠 𝐺𝑒𝑟ä𝑡𝑠 ; 𝐵 ̅ = 𝑁𝑖𝑐ℎ𝑡 𝑎𝑢𝑓𝑏𝑙𝑖𝑛𝑘𝑒𝑛 𝑑𝑒𝑠 𝐺𝑒𝑟ä𝑡𝑠
Wir wissen, dass 15 von 10000 Geldscheinen unecht sind. Damit gilt nach Laplace für Ereignis 𝐴 und für das Komplementärereignis ¯𝐴 folgende Wahrscheinlichkeiten:

Wir wissen, dass Ereignis 𝐵 („Aufblinken des Geräts“) zu 95% (0,95) eintritt, wenn Ereignis 𝐴 ̅ („Schein unecht“) vorausgesetzt wird. Zusätzlich wissen wir, dass Ereignis 𝐵 („Aufblinken des Geräts“) zu 10% (0,1) ebenfalls eintritt, obwohl Ereignis 𝐴 („Schein echt“) zuvor eingetreten ist. Für die bedingten Wahrscheinlichkeiten gilt:
Wollen wir nun die bedingte Wahrscheinlichkeit wissen, wie wahrscheinlich es ist, dass es sich beim Ereignis 𝐵 („Aufblinken des Geräts“) um einen echten (Ereignis 𝐴) oder einen unechten (Ereignis 𝐴 ̅) Geldschein handelt, benötigen wir das Theorem von Bayes, denn wir wollen nun das Ereignis „Aufblinken des Geräts“ voraussetzen:
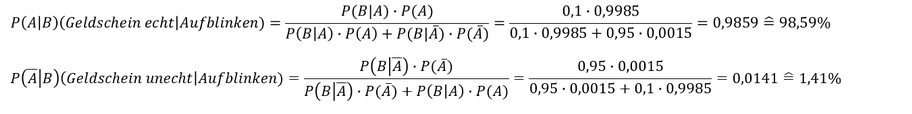
Folglich wissen wir, dass wenn das Gerät aufblinkt der Geldschein zu 98,59% echt und nur zu 1,41% unecht ist. Dieser Sachverhalt lässt sich auch mittels absoluter Zahlen schnell beweisen.
Beweisführung mittels absoluter Zahlen:
Zum Beweis wollen wir die berechneten Wahrscheinlichkeiten nochmals mittels absoluter Zahlen ermitteln. Dazu müssen wir bestimmen, wie oft das Gerät tatsächlich bei 10000 Geldscheinen aufblinken wird. Dazu multiplizieren wir die bedingten Wahrscheinlichkeiten mit den absoluten Anzahlen der echten und unechten Geldscheine:
Anzahl des Aufblinkens bei echten Geldscheinen: 0,1 ∙ 9985 = 998,5 ; Anzahl des Aufblinkens bei unechten Geldscheinen: 0,95 ∙ 15 = 14,25
Bei 10000 Geldscheinen wird das Gerät insgesamt 998,5 + 14,25 = 1012,75 aufblinken, wobei es sich bei 998,5 um echte und nur bei 14,25 Geldscheinen um unechte handelt. Berechnen wir die Wahrscheinlichkeiten nach Laplace:
Wahrscheinlichkeit Schein echt beim Aufblinken: 998,5 / 1012,75 = 09859 = 98,59% ; Wahrscheinlichkeit Schein unecht beim Aufblinken: 14,25 / 1012,75 = 0,0141 = 1,41%
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


