Test für Normalverteilung - Vertiefung der Statistik - Fernuni Hagen
Vertiefung Statistik-Paket > Vertiefung-Statistik > Einstichproben-Testverfahren
Beispielhafte Aufgabe für den 𝝌^𝟐-Anpassungstest:
Eine Stichprobe im Umfang von 𝑁=100 einer unbekannten Grundgesamtheit ergab folgende Häufigkeiten für die einzelnen bereits vorgegebenen Klassen:
Es soll geprüft werden, ob für die Grundgesamtheit von einer Normalverteilung ausgegangen werden kann. Aus den Stichprobenwerten ließ sich als Schätzwert das arithmetische Mittel 𝑥 ̅ = 26,6 und die Varianz 𝜎^2 = 91,2 errechnen.
Wie lautet folglich die passende Nullhypothese für das statistische Testverfahren und kann die Nullhypothese bei einem Signifikanzniveau von 𝛼 = 0,1 abgelehnt werden?
Lösung 𝝌^𝟐-Anpassungstest:
Wahl des Testverfahrens
Es ist nach der Prüfung einer Verteilung gefragt, weshalb der 𝜒^2-Anpassungstest zur Prüfung auf die Normalverteilung verwendet werden muss.
Formulierung der Nullhypothese
Als Nullhypothese ist zu formulieren, dass die Verteilung der Grundgesamtheit die Normalverteilung annimmt. Dabei ist als Nullhypothese der Verteilung die Normalverteilung zu nennen. Mit dem Nichtablehnen der Nullhypothese wird entsprechend von der Verteilung ausgegangen, solange nicht das Gegenteil bewiesen ist:
Prüfgröße/Teststatistik
Zur Ermittlung von 𝜒^2 muss zunächst ermittelt werden, welche Häufigkeiten in den einzelnen Klassen bei einer tatsächlichen Normalverteilung auftreten würden. Dazu gilt es die oberen Klassengrenzen der jeweiligen Klassen zu standardisieren und die Wahrscheinlichkeit für den Eintritt der standardisieren Werte in der Standardnormalverteilung zu bestimmen. Zur Standardisierung ist das arithmetische Mittel 𝑥 ̅ und die Varianz 𝜎^2 zu verwenden. Die Wahrscheinlichkeiten der standardisierten 𝑧-Werte lassen sich dann mit Hilfe der Tabelle der Standardnormalverteilung bestimmen. Um zu den Klassenwahrscheinlichkeiten zu gelangen, gilt es die Wahrscheinlichkeiten der jeweiligen oberen Grenze von der Wahrscheinlichkeit der jeweils unteren Grenze zu subtrahieren:
Prüfgröße/Teststatistik
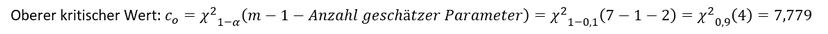
Die Wahrscheinlichkeitswerte der Klassen geben an, wie wahrscheinlich es ist, dass ein Wert bei unterstellter Normalverteilung in die Klasse fällt. Multipliziert man also die jeweilige Wahrscheinlichkeit mit dem Stichprobenumfang 𝑁=100, erhält man die absoluten Häufigkeitswerte für die einzelnen Klassen, wie sie bei einer Normalverteilung auftreten müssten:
Mit den theoretischen Häufigkeiten, die bei einer Normalverteilung auftreten müssten und den empirischen Häufigkeiten, die bei der Stichprobe eingetreten sind, lässt sich nun die Prüfgröße 𝜒^2 ermitteln.
Ermittlung des kritischen Wertes
Es gilt den oberen kritischen Wert des 𝜒^2-Anpassungstest bei einem Signifikanzniveau von 𝛼=0,1 zu bestimmen. Dabei beträgt die Anzahl der Klassen 7, wobei der Freiheitsgrad um den Wert 3 zu vermindern ist. Denn durch die Verwendung der Schätzwerte für das arithmetische Mittel und der Varianz gehen weitere zwei Freiheitsgrade verloren:
Testentscheidung
Da die Prüfgröße unterhalb des oberen kritischen Wertes liegt, kann die Nullhypothese nicht abgelehnt werden:
𝜒^2 = 2,3873 < 𝑐_𝑜 = 7,779 ⇒ Nullhypothese nicht ablehnen/verwerfen
Video "Test für Normalverteilung":
Das Probe-Video behandelt die Thematik "Test für Normalverteilung" des Kurses "Vertiefung der Statistik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Vertiefung Statistik-Paket
18,5 h Lehrvideos
171 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Vertiefung Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Vertiefung der Statistik" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 140 Übungsaufgaben, Übungsklausuren und zur Auffrischung statistischer Grundkenntnisse das "Grundlagen Statistik-Paket" zur Verfügung.
