Korrelationskoeffizient Spearman - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Zweidimensionale Häufigkeitsverteilung
Grundlagen des Korrelationskoeffizienten nach Spearman:
Der Korrelationskoeffizient nach Spearman, auch als Rangkorrelationskoeffizient bezeichnet, stellt eine Maßzahl für den monotonen Zusammenhang zwischen zwei ordinalskalierten Merkmalen dar. Dabei spricht man von einem gleichgesinnten monotonen Zusammenhang, wenn große Werte von Merkmalsausprägungen des einen Merkmals mit großen Werten von Merkmalsausprägungen des anderen Merkmals einhergehen. Ein gegensinniger monotoner Zusammenhang besteht, wenn große Werte des einen Merkmals mit kleinen Werten des anderen Merkmals einhergehen. Obwohl ein linearer Zusammenhang gleichzeitig immer auch monoton ist, bedeutet dies im Umkehrschluss nicht, dass ein monotoner Zusammenhang immer auch linear sein muss. Deshalb lässt sich die Art des Zusammenhangs mit dem Korrelationskoeffizienten nach Spearman nicht eindeutig bestimmen.
Merke: Ein linearer Zusammenhang ist immer monoton. Ein monotoner Zusammenhang ist jedoch nicht immer auch linear. (Exponentielle Zusammenhänge sind monoton, aber nicht linear)
Berechnung des Korrelationskoeffizienten nach Spearman:
Der Korrelationskoeffizient nach Spearman wird mit dem Symbol 𝑟_𝑠 beschrieben, wobei die Berechnung mittels der Bildung von sogenannten Rängen erfolgt. Zur Berechnung des Rangkorrelationskoeffizienten 𝑟_𝑠 sind die jeweiligen ordinalskalierten Merkmalsausprägungen nach ihrer Reihenfolge zu sortieren und entsprechende Ränge 𝑟𝑔 nach der Reihenfolge 1,2,3,… zu verteilen. Die Ränge der jeweiligen Merkmalskombinationen sind voneinander zu subtrahieren, danach zu quadrieren und anschließend komplett zu addieren. Das Ergebnis der Addition ist mit der vereinfachten Formel mit der Zahl 6 zu multiplizieren und dieses Ergebnis ist mit dem Produkt aus Gesamtanzahl aller Merkmalskombinationen 𝑛 mal der quadrierten Gesamtanzahl aller Merkmalskombinationen 𝑛 minus 1 (𝑛^2−1) zu dividieren. Das Ergebnis dieses Quotienten ist von der Zahl 1 zu subtrahieren um schließlich zum Rangkorrelationskoeffizienten zu gelangen:
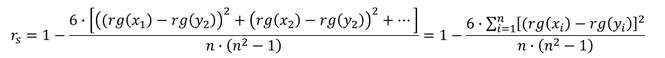
Oftmals wird die Subtraktion der Ränge mit der Variable: 𝑑_𝑖=𝑟𝑔(𝑥_𝑖 )−𝑟𝑔(𝑦_𝑖) benannt, sodass die Formel auch verkürzt aufgeschrieben werden kann:
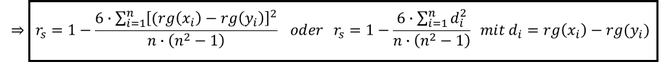
Interpretation der Maßzahl des Korrelationskoeffizienten nach Spearman:
Der Korrelationskoeffizient nach Spearman kann ausschließlich Werte im Bereich von −1 und 1 [ −1 ≤ 𝑟_𝑠 ≤ 1 ] annehmen. Dabei können die Extremwerte wie folgt für den monotonen Zusammenhang zwischen zwei Merkmalen interpretieren werden, wobei Werte dazwischen wieder die Richtung umso mehr andeuten, je näher sie an den Extremwerten liegen:
𝑟_𝑠 = −1: Eindeutiger gegensinniger monotoner Zusammenhang
𝑟_𝑠 = 0: Kein monotoner Zusammenhang
𝑟_𝑠 = 1: Eindeutiger gleichsinniger monotoner Zusammenhang
Video "Korrelationskoeffizient Spearman":
Das Probe-Video behandelt die Thematik "Korrelationskoeffizient Spearman" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Beispielhafte Bestimmungen des Korrelationskoeffizienten nach Spearman:
Zur Veranschaulichung der Berechnung des Korrelationskoeffizienten nach Spearman soll die Bestimmung anhand zweier Merkmale 𝑋 und 𝑌 erfolgen. Dabei soll das Merkmal 𝑋 die Leistung im Kugelstoßen in Meter und das Merkmal 𝑌 dagegen die Leistung im Weitsprung in Meter angeben. Insgesamt ergab die Erhebung folgende Merkmalskombinationen:

Bei den angegebenen Werten handelt es sich zwar um metrisch skalierte Werte, wir wollen aber dennoch den Rangkorrelationskoeffizienten berechnen. Zur Berechnung des Rangkorrelationskoeffizienten müssen wir die jeweiligen Merkmalsausprägungen der Merkmale 𝑋 und 𝑌 sortieren und anschließend der Reihenfolge nach einen Rang zuordnen:
Sortierung der Merkmalsausprägungen 𝑥_𝑖 nach der Reihenfolge und Rangzuweisung 𝑟𝑔(𝑥_𝑖):

Sortierung der Merkmalsausprägungen 𝑦_𝑖 nach der Reihenfolge und Rangzuweisung 𝑟𝑔(𝑦_𝑖):

Die Merkmalsausprägungen der Merkmalskombinationen sind nun durch die zugeordneten Ränge zu ersetzen. Mittels der Ränge kann die Formel des Rangkorrelations-koeffizienten angewandt werden:

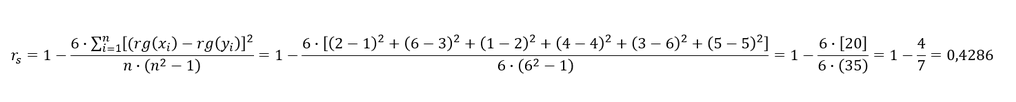
Zwischen den Merkmalen 𝑋 und 𝑌 besteht kein wirklicher monotoner Zusammenhang.
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


