Klassierung von Merkmalsausprägungen - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Eindimensionale Häufigkeitsverteilung
Klassierung zur Übersichtlichkeit des Datenmaterials:
Neben der Einordnung und Umwandlung von Datenmaterial bedarf es je nach Datenmenge zur Übersichtlichkeit der Zusammenfassung einzelner Merkmalsausprägungen zu einer Gruppe bzw. Klasse von benachbarten Merkmalsausprägungen. Die Gruppierung/Klassierung von benachbarten Merkmalsausprägungen geht meist mit einem Informationsverlust einher, da die einzelnen Merkmalsausprägungen innerhalb der Gruppierung/Klasse oft nicht mehr festgestellt werden können. Bei der Gruppierung/Klassierung ist darauf zu achten, dass die Gruppen/Klassen möglichst einheitlich gebildet werden. Man spricht dabei von der sogenannten gleichen Klassenbreite.
Beispiel einer Klassierung:
Werden Daten über 200 Personen und deren Größe erhoben, erhält man sehr viele unterschiedliche Zentimetergrößen die nahe beieinander liegen. Eine Auflistung aller Werte in Zentimeter könnte sehr unübersichtlich ausfallen. Deshalb könnte hier eine Klassierung (Gruppierung) sinnvoll sein, indem man beispielsweise Merkmalsausprägungen innerhalb von jeweils 10cm zu einer Klasse (Gruppe) zusammenfasst:

Merke: Stimmt die obere Grenze einer Klasse mit der unteren Grenze einer größeren Klasse überein, ist ein Wert der auf die Klassengrenze fällt, immer der Klasse mit der oberen Grenze bzw. der „kleineren“ Klasse zuzuordnen. Eine Person mit der Größe von 170cm würde also der Klasse [160;170] zugeordnet werden.
Offene Randklassen bei einer Klassierung:
Je nachdem, wie viele Merkmalswerte vorliegen und wie groß die Unterschiede zwischen den einzelnen Merkmalswerten sind, kann es durchaus vorkommen, dass es einer enormen Anzahl an Klassen/Gruppen bedarf. Als Faustregel gilt, dass die Anzahl an Klassen nicht die Zahl 20 überschreiten sollte, da ansonsten die eigentliche Aufgabe der Klassierung, nämlich die Schaffung von Übersichtlichkeit, verloren geht. Neben der Begrenzung der Anzahl von Klassen können aber auch offene Randklassen der Schaffung von Übersichtlichkeit dienen. Liegen einige extreme Merkmalswerte vor, die entweder sehr niedrig oder sehr hoch sind, ist es durchaus sinnvoll, die Randklasse/Randgruppen offen zu lassen und sie durch ein größer/kleiner Zeichen zu begrenzen.
Beispiel einer Klassierung mit offenen Randklassen:
Kommen bei unseren 200 Personen vereinzelt extreme Werte vor, wie beispielsweise die Größe von 50cm oder von 210cm, ist es sinnvoll die Randklassen offen zu lassen:

Video "Klassierung von Merkmalsausprägungen":
Das Probe-Video behandelt die Thematik "Klassierung von Merkmalsausprägungen" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Klassengrenzen, Klassenmitte und Klassenbreite
Klassengrenzen:

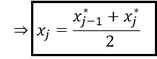
Der unterste und oberste Wert einer Klasse (Gruppe) wird als Klassengrenze bezeichnet. Die untere Klassengrenze wird durch die Variable 𝑥_(𝑗−1)^∗ und die obere Grenze durch die Variable 𝑥_𝑗^∗ definiert. Bei offenen Randklassen ist entweder die obere oder untere Klassengrenze nicht vorhanden.
Beispiele von Klassengrenzen:

Klassenmitte:
Mittels der Klassengrenzen lässt sich auch die Klassenmitte (𝑥_𝑗) errechnen. Dazu sind die beiden Klassengrenzen zusammenzuaddieren und durch 2 zu dividieren:
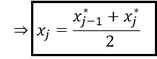
Beispiele von Klassenmitten:
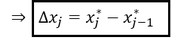
Klassenmitte der Klasse [150 ; 160]: 𝑥_𝑗 = (150 + 160) / 2 = 155
Klassenmitte der Klasse [170 ; 180]: 𝑥_𝑗 = (170 + 180) / 2 = 175
Klassenmitte der Klasse [ > 190 ]: 𝑥_𝑗 = (190 + ???) / 2 = ?
ACHTUNG: Die Klassenmitte einer offenen Randklasse kann nicht ohne Probleme bestimmt werden, da entweder die untere oder obere Grenze fehlt. Als Lösung kommen nur die Angabe des nächsten Wertes bei gleichen Abständen aller Klassenmitten in Frage, was im Beispiel 195 bedeuten würde, eine Schätzung oder eine Berechnung des Mittelwertes aus den ursprünglichen tatsächlichen Merkmalswerten.
Klassenbreite:
Neben der Klassenmitte ist auch die Klassenbreite (∆𝑥_𝑗) von Bedeutung. Zur Berechnung der Klassenbreite ist die obere Grenze von der unteren abzuziehen:
Beispiele von Klassenbreiten:
Klassenbreite der Klasse [150 ; 160]: ∆𝑥_𝑗 = 160 − 150 = 10
Klassenbreite der Klasse [170 ; 180]: ∆𝑥_𝑗 = 180 − 170 = 10
Merke: Klassenbreiten sollten möglichst einheitlich gewählt werden. Auch hier treten Probleme bei offenen Randklassen auf.
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


