Differenzengleichungen - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Differential- und Differenzengleichungen
Grundlagen von Folgen: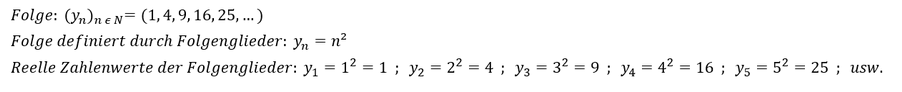
Eine Zahlenfolge von reellen Zahlen wird in der Mathematik kurz als Folge bezeichnet. Die einzelnen reellen Zahlen der Zahlenfolge stellen die (Folgen-)Glieder der Folge dar, wobei die erste Zahl der Folge das erste Folgenglied, die zweite Zahl der Folge das zweite Folgenglied usw. ist. Eine Folge kann durch seine Folgenglieder definiert sein, wobei wir in Anlehnung an die Differentialgleichungen eine Folge mit 𝑦_𝑛 bezeichnen wollen, wobei 𝑛 das 𝑛-te Folgenglied bezeichnet. Zum besseren Verständnis wollen wir uns eine beispielhafte Folge 𝑦_𝑛 definiert durch seine Folgenglieder 𝑛 anschauen:
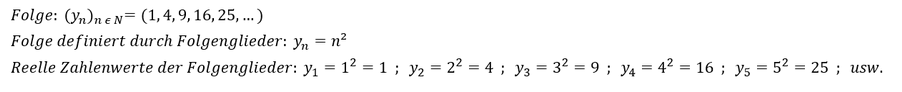
Grundlagen der ersten Differenzenfolgen:
Die erste Differenzenfolge gibt das Änderungsverhalten einer Folge wieder. Das Änderungsverhalten einer Folge entspricht dabei der Differenz zwischen den jeweils aufeinanderfolgenden Folgegliedern. Zur Ermittlung des Änderungsverhaltens eines Folgengliedes 𝑛, gilt es vom nächsten Folgenglied 𝑛+1 das Folgenglied 𝑛 abzuziehen. Für eine erste Differenzenfolge, die mit ∆𝑦_𝑛 bezeichnet wird, gilt daher allgemein: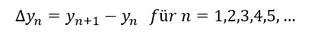
Beispiel:
Die erste Differenzenfolge unserer beispielhaften Folge lautet:
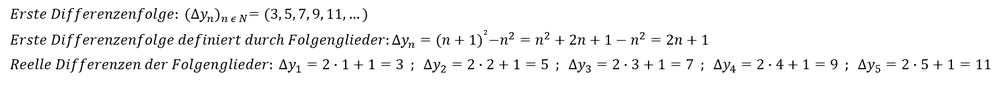
Merke: Die Differenzenfolge mit ihrem Änderungsverhalten der Folge ist angelehnt an die Ableitung einer Funktion, die das Änderungsverhalten einer stetigen Funktion wiedergibt.
Grundlagen höherer Differenzenfolgen: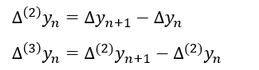
In Anlehnung an die höheren Ableitungen einer Funktion, gibt es auch höhere zweite, dritte, usw. Differenzenfolgen, die jeweils das Änderungsverhalten der vorherigen Differenzenfolgen angeben. Die Angabe, um welche Differenzenfolge es sich handelt, erfolgt als Hochzahl in Klammern hinter dem Differenzzeichen ∆ (∆^((2) ) 𝑦_𝑛, ∆^((3) ) 𝑦_𝑛,..). Zur Ermittlung einer höheren Differenzenfolge gilt es vom nächsten Differenzfolgenglied ∆𝑦_(𝑛+1) das Differenzfolgenglied ∆𝑦_𝑛 abzuziehen. Für eine zweite und dritte Differenzenfolge, die mit ∆^((2) ) 𝑦_𝑛 und ∆^((3) ) 𝑦_𝑛 bezeichnet werden, gilt daher allgemein:
Video "Differenzengleichungen":
Das Probe-Video behandelt die Thematik "Differenzengleichungen" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Berechnung von Differenzenfolgen:
Die Vorgehensweise zur Berechnung von Differenzenfolgen lässt sich am einfachsten anhand eines Beispiels veranschaulichen. Deshalb wollen wir die erste, zweite und dritte Differenzenfolge anhand der folgenden beispielhaften Folge bestimmen:
Erste Differenzenfolge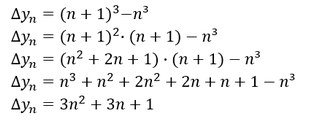
Zur Ermittlung der ersten Differenzenfolge ∆𝑦_𝑛 gilt es zunächst die Folge aufzuschreiben, bei der 𝑛 durch 𝑛+1 ersetzt wird. Davon abzuziehen ist die unveränderte Folge:
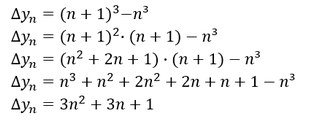
Zweite Differenzenfolge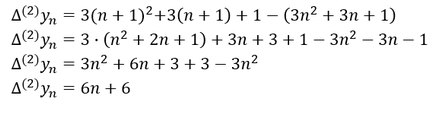
Zur Ermittlung der zweiten Differenzenfolge ∆^((2)) 𝑦_𝑛 gilt es zunächst die erste Differenzenfolge aufzuschreiben, bei der 𝑛 durch 𝑛+1 ersetzt wird. Davon abzuziehen ist die unveränderte erste Differenzenfolge:
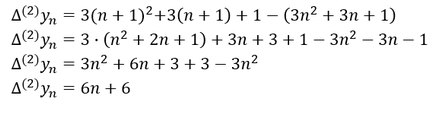
Dritte Differenzenfolge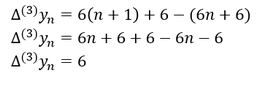
Zur Ermittlung der dritten Differenzenfolge ∆^((3)) 𝑦_𝑛 gilt es zunächst die zweite Differenzenfolge aufzuschreiben, bei der 𝑛 durch 𝑛+1 ersetzt wird. Davon abzuziehen ist die unveränderte zweite Differenzenfolge:
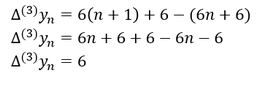
Bestimmung von Folgengliedern einer Differenzenfolge: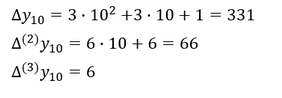
Zur Bestimmung eines bestimmten Folgengliedes einer Differenzenfolge ist dieses Folgenglied für 𝑛 in die Differenzenfolge einzusetzen. Wir wollen das 10. Glied für die erste, zweite und dritte Differenzenfolge ermitteln:
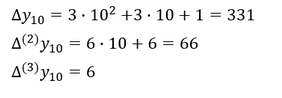
Vertiefung Wirtschaftsmathematik-Paket
Klausurlösungen
Live-Webinare
Übungen (optional)
20 h Lehrvideos
196 Skriptseiten
FormelsammlungDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
