Anfangswertproblem - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Differential- und Differenzengleichungen
Grundlagen des Anfangswertproblems für Differentialgleichungen:
Eine Differentialgleichung gibt eine Beziehung zwischen einer Funktion und ihren Ableitungen an. Da beim Ableiten einer Funktion die Konstanten der Funktion wegfallen, besitzt die Lösungsgleichung einer Differentialgleichung immer eine beliebige Konstante 𝑐, wie wir sie aus der Integralrechnung kennen. Die Konstante 𝑐 einer Lösungsgleichung kann jedoch eindeutig bestimmt werden, wenn ein Punkt bekannt ist, durch den die Lösungsgleichung der Differentialgleichung verlaufen soll. Die Vorgabe eines Punktes, durch den die Lösungsgleichung der Differentialgleichung verlaufen soll, bezeichnet man dabei als Anfangsbedingung. Die Angabe einer Differentialgleichung mit einer Anfangsbedingung bezeichnet man dann als Anfangswertproblem für die Differentialgleichung.
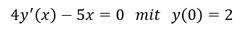
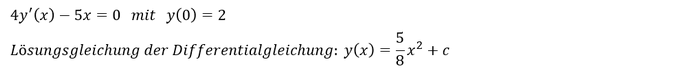

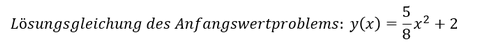
Beispiel
Ein Anfangswertproblem für eine Differentialgleichung könnte wie folgt aussehen:
Die angegebene Anfangsbedingung 𝑦(0) = 2 besagt, dass sich die Lösungsgleichung der Differentialgleichung beim Einsetzen von 𝑥 = 0 der Funktionswert zu y = 2 ergibt. Folglich verläuft die Lösungsgleichung der Differentialgleichung durch den Punkt (0 , 2).
Allgemeine Lösung eines Anfangswertproblems für Differentialgleichungen:
Zur Lösung eines Anfangswertproblems für Differentialgleichungen gilt es zunächst die Lösungsgleichung der Differentialgleichung ganz allgemein mit der beliebigen Konstanten 𝑐 zu entwickeln. Um die Konstante 𝑐 der Lösungsgleichung der Differentialgleichung dann eindeutig bestimmten zu können, werden die Variablen 𝑥 der Lösungsgleichung durch den 𝑥-Wert und der Funktionswert 𝑦(𝑥) durch den 𝑦-Wert des angegebenen Punktes ersetzt. Die Lösungsgleichung der Differentialgleichung enthält dann nur noch die beliebige Konstante 𝑐, nach der umgestellt werden kann.
Beispiel
Wir wollen das obige Anfangswertproblem für die Differentialgleichung lösen, wobei die Lösungsgleichung der Differentialgleichung 𝑦(𝑥) vorgegeben sein soll:
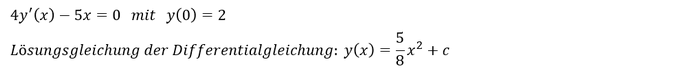
Zur Ermittlung der Lösungsgleichung des Anfangswertproblems der Differentialgleichung ist 𝑥 = 0 und 𝑦(𝑥) = 2 zu setzten und nach 𝑐 umzustellen:

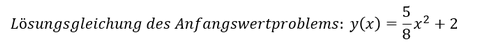
Video "Anfangswertproblem":
Das Probe-Video behandelt die Thematik "Anfangswertproblem" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Vertiefung Wirtschaftsmathematik-Paket
Das Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.


